[vc_row][vc_column][vc_column_text el_id= »objectif-1″]
Taux de variation et Coefficient directeur
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Le taux de variation d’une fonction \(f\) entre \(a\) et \(b\) vaut
\(\displaystyle m=\frac{f(b)-f(a)}{b-a}\)
Le taux de variation d’une fonction \(f\) en \(a\) vaut
\(\displaystyle m=\frac{f(a+h)-f(a)}{h}\)
(on a remplacé \(b\) par \(a+h\) )[/vc_column_text][vc_column_text el_class= »proprietepremieresthr propriete »]Une droite \((AB)\) a pour équation \(f(x)=mx+p\) ;
\(m\) est le coefficient directeur ; il vaut
\(\displaystyle m=\frac{y_B-y_A}{x_B-x_A}\)
(c’est le taux de variation de \(f\) entre \(x_A\) et \(x_B\) )[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-2″]
Nombre dérivé et tangente
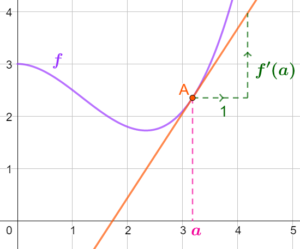
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Si \(f\) est une fonction, sa courbe est \(\mathscr{C}\) et \(A\) est un point de la courbe qui a pour abscisse \(a\).
Alors le nombre dérivé est le coefficient directeur de la tangente à la courbe au point \(A\)
 [/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]
Quizz
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Plan de travail
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vTq6KOpT6_Jr3gQfAJCv0T-bpTAIvP33fbr0MHIC3Ix2H_eJIKRCTQb-hqYOGpxuhO0seljaqKGCrw6/pub?w=960&h=720″][/vc_column][/vc_row]
