[vc_row][vc_column][vc_column_text css= » » el_id= »objectif-1″]
Fréquences
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Propriété
La fréquence d’une population d’effectif \(n_A\) dans une population totale d’effectif \(n_E\) vaut \(\frac{n_A}{n_E}\)
Exemple
La fréquence d’usagers du train vaut \(\frac{73}{115}\approx 0,635\)[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]
Quizz
Ci-dessous la répartition des hôtels en Franche-Comté :
[/vc_column_text][vc_column_text]
[/vc_column_text][vc_column_text]
Fréquences marginales
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Définition
Dans un tableau croisé, la fréquence marginale d’une population est la fréquence de la population dans une marge (ligne ou colonne « Total« ).
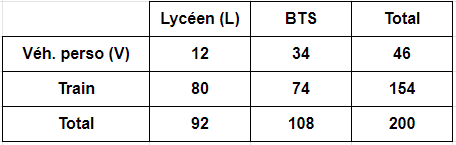
Fréquence (marginale) de lycéens : \(\displaystyle \frac{92}{200}\)[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Fréquences conditionnelles
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Dans un tableau croisé, la fréquence conditionnelle d’une population A dans une population B se calcule à l’intérieur d’une ligne ou d’une colonne ; elle est notée \(f_B(A)\) (on dit \(f\) de \(A\) sachant \(B\))
Dans le tableau précédent, parmi les lycéens, la fréquence d’élèves prenant leur véhicule personnel vaut :
\(f_L(V)=\frac{12}{92}\)[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text][/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text css= » »]
Parcours
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » css= » » custom_src= »https://docs.google.com/drawings/d/19GsO0l2DQdnTgpTsBpwqkDeFTMv0lfBxgXXfFZ93GJU/edit?usp=sharing »][/vc_column][/vc_row]