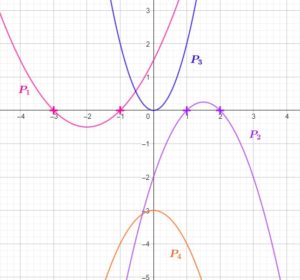
Fonction du second degré
Définition : Une fonction du second degré s’écrit
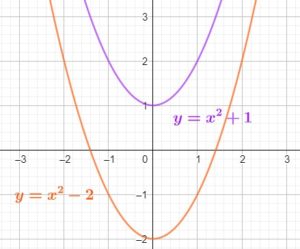
Exemples :
La parabole – éléments caractéristiques
Une fonction du second degré
Cette parabole possède un axe de symétrie vertical qui passe par son sommet.
Exemples :
- avec
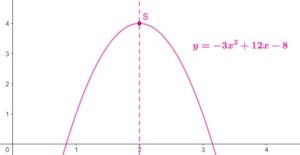
- avec
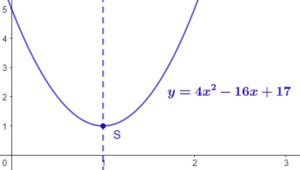
Les 3 formes
La parabole qui représente
- tournée vers le haut si
- tournée vers le bas si
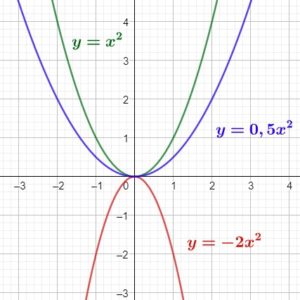
La parabole qui représente
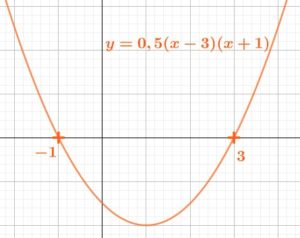
La parabole qui représente
Quizz