Taux de variation et Coefficient directeur

Le taux de variation d’une fonction $f$ entre $a$ et $b$ vaut
$${\displaystyle m=\frac{f(b)-f(a)}{b-a}}$$
Le taux de variation d’une fonction $f$ en $a$ vaut
$${\displaystyle m=\frac{f(a+h)-f(a)}{h}}$$
(on a remplacé $b$ par $a+h$ )

Une droite $(AB)$ a pour équation $f(x)=mx+p$ ;
$m$ est le coefficient directeur ; il vaut
$${\displaystyle m=\frac{y_B-y_A}{x_B-x_A}}$$
(c’est le taux de variation de $f$ entre $x_A$ et $x_B$ )

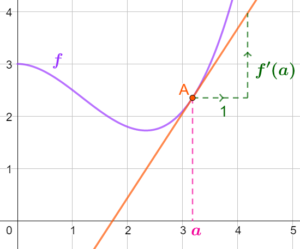
Nombre dérivé et tangente

Si $f$ est une fonction,
$\mathcal{C}$ sa courbe
et $A$ est un point de la courbe qui a pour abscisse $a$.

Alors le nombre dérivé est le coefficient directeur de la tangente à la courbe au point $A$

Quizz