[vc_row][vc_column][vc_column_text el_id= »objectif-1″]

Définition

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Une fonction affine s’écrit $f(x)=mx+p$

$m$ s’appelle le coefficient directeur.

$p$ s’appelle l’ordonnée à l’origine.[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]

Taux d’accroissement

Dans le cas des fonctions affines, le taux d’accroissement ${\displaystyle \frac{f(b)-f(a)}{b-a}}$ est constant (et égal à $m$ )[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Si $p=0$ (c’est-à-dire $f(x)=mx$ alors $f$ est linéaire.

Si $m=0$ (c’est-à-dire $f(x)=p$ alors $f$ est constante.[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]

Quizz

[/vc_column_text][/vc_column][vc_column width= »1/2″][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-3″]

Représentation graphique

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Une fonction affine est représentée par une droite.

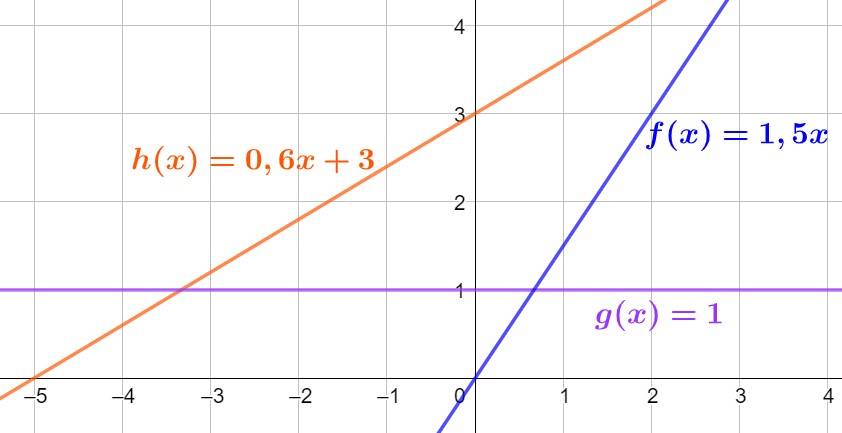
Les trois fonctions sont affines, la fonction $f$ est en plus linéaire, la fonction $g$ est en plus constante[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]

Quizz

On considère une fonction affine dans un graphique.

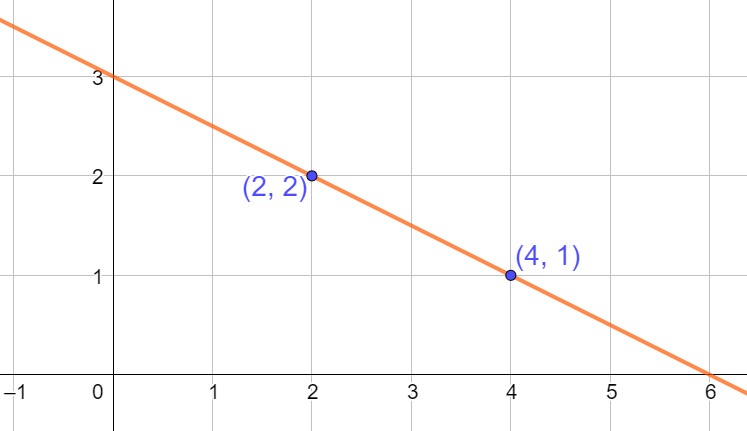
Répondre aux quatre questions suivantes

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-4″]

Variations et signe

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text el_class= »proprieteseconde propriete »]Les variations d’une fonction affine $x\mapsto mx+p$ dépendent du signe de $m$…[/vc_column_text][vc_row_inner][vc_column_inner width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]

… croissante lorsque $m$ est positif

 

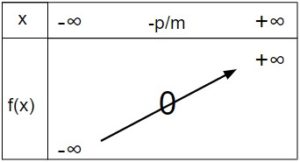
Dans ce cas, la fonction $f$ est négative sur l’intervalle $]-\mathrm{\infty };-\frac{p}{m}[$ et positive sur l’intervalle $]-\frac{p}{m};+\mathrm{\infty }[$[/vc_column_text][/vc_column_inner][vc_column_inner width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]

… décroissante lorsque $m$ est négatif

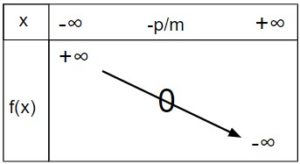
Dans ce cas, la fonction $f$ est positive sur l’intervalle $]-\mathrm{\infty };-\frac{p}{m}[$ et négative sur l’intervalle $]-\frac{p}{m};+\mathrm{\infty }[$[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner][vc_column_inner][vc_column_text el_class= »proprieteseconde propriete »]Dans tous les cas, la fonction s’annule pour $x={\displaystyle -\frac{p}{m}}$[/vc_column_text][/vc_column_inner][/vc_row_inner][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]

Quizz

Répondre aux questions suivantes

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Synthèses :

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vSxpuPuXnVV4nt7UyapI2yVQRqCkMoBjRxcgQIlfwalCUZDIIn_KPfYJ28XPg_r6UQiS3dlKjhHPWGv/pub?w=960&h=720″][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vRKKO8BXkNqxt2tpXENMYX3JLBwsihopdFWohYwxV00GsL6iOxmVgU58IlkYzOr0wu7SV95obQG4piR/pub?w=960&h=720″][/vc_column][/vc_row]