[vc_row][vc_column][vc_column_text el_id= »objectif-1″]
Rappels
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text el_class= »proprietepremieresthr propriete »]Lors d’une expérience aléatoire, on associe un événement à une quantité (par exemple un gain). La variable X qui représente cette quantité est appelée variable aléatoire.
La probabilité que la variable aléatoire prenne la valeur a s’écrit P(X=a)[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Exemple
On lance un dé à 20 faces.
- Si on fait entre 1 et 10, on marque 5 points ;
- si on fait entre 11 et 17 on marque 10 points ;
- si on fait 18 ou plus, on marque 15 points.
On note X la variable aléatoire qui compte le nombre de points marqués.
Le tableau suivant s’appelle al loi de probabilité de X
| a | 5 | 10 | 15 |
| P(X=a) | 0,5 | 0,35 | 0,15 |
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-1″]
Espérance d’une v.a.
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Formule (
[/vc_column_text][vc_column_text el_class= »proprietepremieresthr propriete »]Dans l’exemple précédent, l’espérance vaut
Cela signifie que sur un grand nombre d’essais, on marque en moyenne 10,375 points par lancer.[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-3″]
Loi binomiale
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]
Coefficient binomial
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Le coefficient binomial
Exemples :
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]
Calculer des coefficients binomiaux à l’aide du triangle de Pascal
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]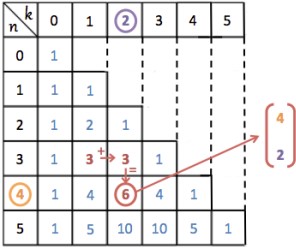 [/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]
Calculer une probabilité dans le cas d’une loi binomiale
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Lors de la répétition de n expériences suivant le schéma de Bernoulli (Succès
où
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Plan de travail
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vSKkWaqyfAdA-5-QnZ9H5eEbzor_Q2DETSiqfUWS3h5GzhmAdpHV1r39BzX2aBzuvVxA6PfRGgNK1xG/pub?w=960&h=720″][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Synthèse
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vTUy9V4q691qAjILjiRt6VgiIknHEF_fqsPDRTcK6uX1XfXoUWAESLaicMUenpLz-T49QxOAfSNPO28/pub?w=960&h=720″][/vc_column][/vc_row]
