Fonction du second degré
Définition :
Une fonction du second degré s’écrit \(f(x)=ax^2+bx+c\) où \(a,b,c \) sont trois nombres donnés.
Exemples :
\(x^2+4\) (\(a\) vaut 1, \(b\) vaut 0 et \(c\) vaut 4)
\(3x^2-2x+5\) (\(a\) vaut 3, \(b\) vaut -2 et \(c\) vaut 5)
La parabole – éléments caractéristiques
Propriété :
Une fonction du second degré $f : x \mapsto ax^2+bx+c$
est représentée sous la forme d’une parabole, dont l’orientation dépend du signe de $a$.
Cette parabole possède un axe de symétrie vertical qui passe par son sommet.
Exemples :
- avec \(a\) négatif (il vaut -3), sommet \(S(2;4)\) et axe de symétrie d’équation \(x=2\)
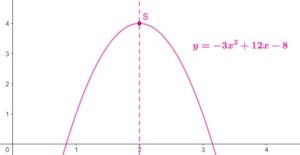
- avec \(a\) positif (il vaut 4), sommet \(S(1;1)\) et axe de symétrie d’équation \(x=1\)
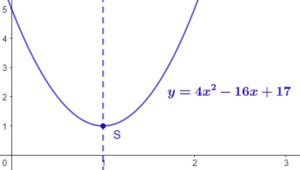
Les 3 formes
\(f(x)=ax^2\)
La parabole qui représente \(y=ax^2\) passe par l’origine et est :
- tournée vers le haut si \(a\) est positif (courbes bleue et verte)
- tournée vers le bas si \(a\) est négatif (courbe rouge)
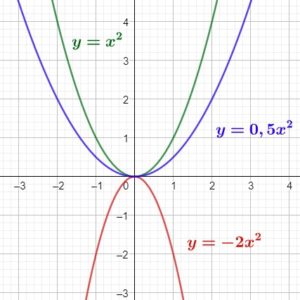
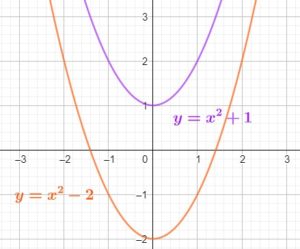
\(f(x)=ax^2+b\)
La parabole qui représente \(y=ax^2+b\) s’obtient de la précédente par un décalage vertical de (b) unités
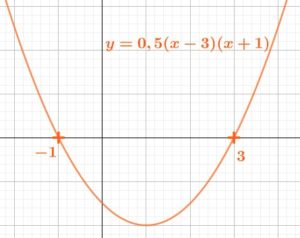
\(f(x)=a(x-x_1)(x-x_2)\)
La parabole qui représente \(y=a(x-x_1)(x-x_2)\) coupe l’axe des abscisses aux valeurs (x_1) et (x_2) (appelées racines de la fonction)
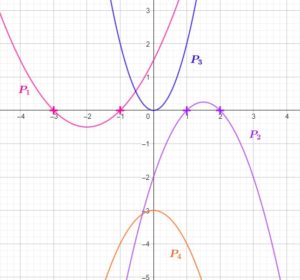
Quizz
\(P_1\), \(P_2\), \(P_3\), \(P_4\) représentent quatre fonctions polynômes de degré 2.