Suites arithmétiques
Une suite arithmétique de raison \(r\) est définie par :
- la relation de récurrence $u_{n+1}=u_n+r$
- son expression explicite $u_n=u_0+nr$
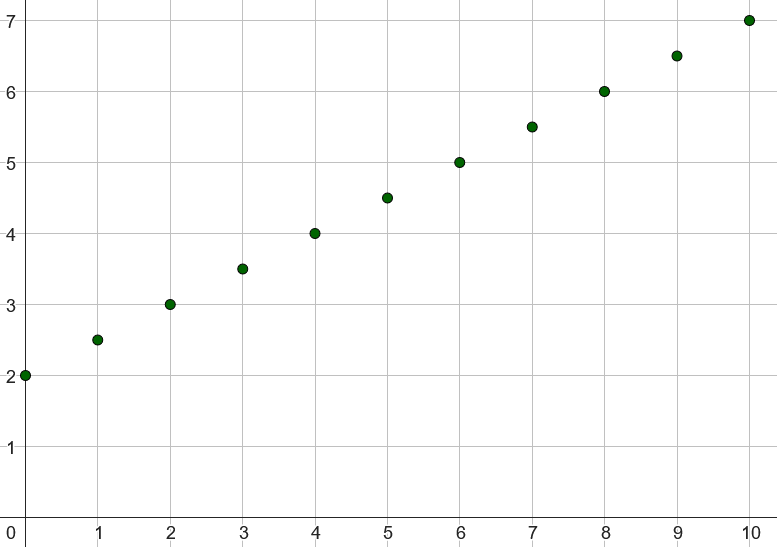
Représentation graphique : les points sont alignés.
Ici, la représentation de la suite de premier terme 2 et de raison 0,5 ($u_n=2+0,5n$)
Variations
Si $r$ est positif, la suite est croissante
Si $r$ est négatif, la suite est décroissante
Somme des termes
$1+2+\dots+n=\dfrac{n(n+1)}{2}$
Et pour tout suite arithmétique de raison $r$ :
$u_0+u_1+\dots+u_n=(n+1)\dfrac{u_0+u_n}{2}$
$u_r+u_{r+1}+\dots+u_n= (n-r+1)\dfrac{u_r+u_n}{2}$
Suites géométriques
Une suite géométrique de raison \(q\) est définie par :
- la relation de récurrence $u_{n+1}=u_n\times q$
- son expression explicite $u_n=u_0\times q^n$
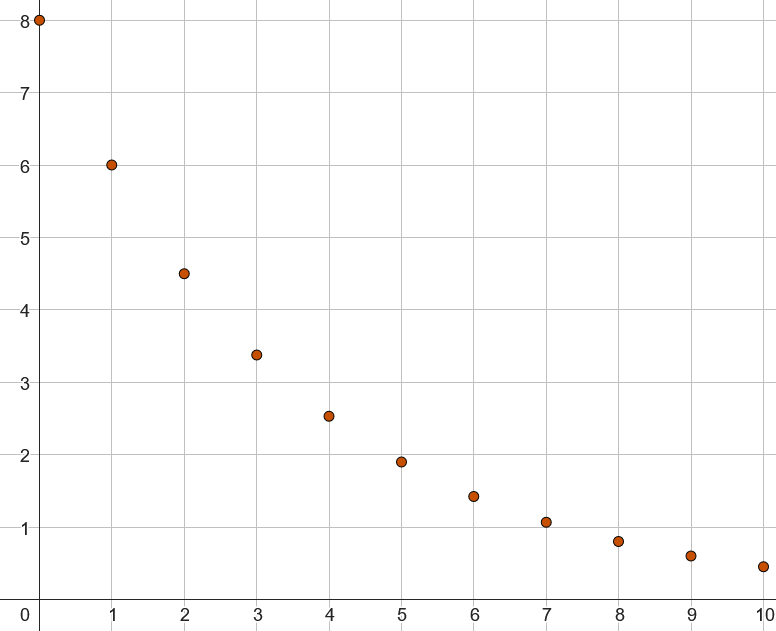
Représentation graphique : les points ne sont pas alignés.
Ici, la représentation de la suite de premier terme 2 et de raison 0,5 ($u_n=2\times0,5^n$).
On verra par la suite que les points suivent une courbe exponentielle.
Variations
Pour une suite géométrique de premier terme $u_0$ positif :
Si $q>1$, la suite est croissante
Si $0<q<1$, la suite est décroissante
Somme des termes
$1+q+q^2+\dots+q^n=\dfrac{q^n-1}{q-1}$
Et pour tout suite géométrique de raison $q$ :
$u_0+u_1+\dots+u_n=u_0\dfrac{q^{n+1}-1}{q-1}$
$u_r+u_{r+1}+\dots+u_n= u_r\dfrac{q^{n-r+1}-1}{q-1}$
