D’abord, un peu d’histoire

Taux de variation et Coefficient directeur

Le taux de variation d’une fonction $f$ entre $a$ et $b$ vaut
$${\displaystyle m=\frac{f(b)-f(a)}{b-a}}$$
Le taux de variation d’une fonction $f$ en $a$ vaut
$${\displaystyle m=\frac{f(a+h)-f(a)}{h}}$$
(on a remplacé $b$ par $a+h$ )

Une droite $(AB)$ a pour équation $f(x)=mx+p$ ;
$m$ est le coefficient directeur ; il vaut
$${\displaystyle m=\frac{y_B-y_A}{x_B-x_A}}$$
(c’est le taux de variation de $f$ entre $x_A$ et $x_B$ )

Nombre dérivé et tangente

Si $f$ est une fonction,
$\mathcal{C}$ sa courbe
et $A$ est un point de la courbe qui a pour abscisse $a$.

Alors le nombre dérivé est le coefficient directeur de la tangente à la courbe au point $A$

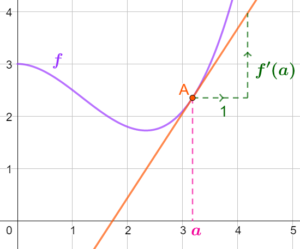
En pratique

Quizz

Équation de la tangente

Application

Fonction dérivée

En associant à tout nombre $x$ le nombre dérivé $f^{\prime }(x)$, on construit une fonction appelée fonction dérivée de $f$ et notée $f^{\prime }(x)$.

Tableau des fonctions dérivées des fonctions de référence

Fonction	Dérivée
k (constante)	0
$ax+b$ (fct affine)	$a$
$x^2$	$2x$
$x^n$	$n{x}^{n-1}$
${\displaystyle \frac{1}{x}}$	${\displaystyle \frac{-1}{x^2}}$
${\displaystyle \frac{1}{x^n}}$	${\displaystyle \frac{-n}{x^{n+1}}}$
$\sqrt{x}$	${\displaystyle \frac{1}{2\sqrt{x}}}$

Tableau des opérations sur les fonctions dérivées

$u$ et $v$ sont deux fonctions	leurs dérivées sont $u^{\prime }$ et $v^{\prime }$
$k\times u$ ($k$ est une constante)	$k\times u^{\prime }$
$u+v$ (somme)	$u^{\prime }+v^{\prime }$
$uv$ (produit)	$u^{\prime }v+v^{\prime }u$ (attention ce n’est pas intuitif ! et en plus il y a un plus !)
${\displaystyle \frac{u}{v}}$	${\displaystyle \frac{-v^{\prime }}{v^2}}$ (pas intuitif non plus, et il y a un moins)
${\displaystyle \frac{u}{v}}$	${\displaystyle \frac{u^{\prime }v-v^{\prime }u}{v^2}}$ (pas intuitif non plus, et il y a encore un moins)
$u^n$	$n{u}^{\prime }{u}^{n-1}$
$\sqrt{u}$	${\displaystyle \frac{u^{\prime }}{2\sqrt{u}}}$

Exemple : Si $f(x)=x^2(5x-4)$ alors la dérivée est
$$\begin{array}{rlrl}{f}^{\prime }(x)& =2x(5x-4)+5\times x^2& \text{ avec }& u=x^2\text{ et }v=5x-4\\ & =10x^2-8x+5x^2& & u^{\prime }=2x{v}^{\prime }=5\\ & =15x^2-8x\end{array}$$

Des exemples en vidéo