[vc_row][vc_column][vc_column_text el_id= »objectif-1″]

Fonction de degré 3 – Définition

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Une fonction du second degré s’écrit \(f(x)=ax^3+bx^2+cx+d\) où \(a,b,c \) sont trois nombres donnés.[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Exemples :

• \(x^3-x\) (\(a\) vaut 1, \(b\) vaut 0, \(c\) vaut -1 et \(d\) vaut 0)
• \(2x^3-x^2+4x+7\) (\(a\) vaut 2, \(b\) vaut -1, \(c\) vaut 4 et \(d\) vaut 7)

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]L’équation \(x^3=c\) possède une solution, la racine cubique de \(c\), notée \(\sqrt[3]{c}\) (ou \(c^{\frac{1}{3}}\) )[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-2″]

Fonction \(x \mapsto ax^3\) – variations et courbe

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]La fonctions \(x \mapsto ax^3\) est :

• croissante lorsque \(a\) est positif
• décroissante lorsque \(a\) est négatif

[/vc_column_text][vc_row_inner][vc_column_inner width= »1/2″][vc_column_text]

Exemple avec \(a\) négatif (il vaut -3)

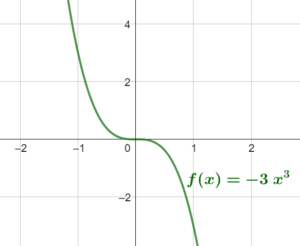[/vc_column_text][/vc_column_inner][vc_column_inner width= »1/2″][vc_column_text]

Exemple avec \(a\) positif (il vaut 4)

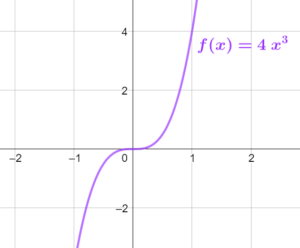[/vc_column_text][/vc_column_inner][/vc_row_inner][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-3″]

Racines, forme factorisée \(a(x-x_1)(x-x_2)(x-x_3)\)

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Une fonction de degré 3 qui admet 3 racines \(x_1, x_2\) et \(x_3\) (c’est-à-dire que l’équation \(f(x)=0\) possède 3 solutions) s’écrit sous forme factorisée :

\(f(x)=a(x-x_1)(x-x_2)(x-x_3)\)

 

On utilise alors un tableau de signe pour chaque facteur pour connaître le signe de la fonction \(f\) (voir page 88 du manuel)[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Synthèse :

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vRcUvJIFR_3sRyZAymTs4CM8Z23-cHMNZcTzYouHmYIOyOT5DR7huw2vkDOW1HfbgVBXZoA2l0xfq1S/pub?w=960&h=720″][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vS9UJq863jHIVHlIHCYlNiIOjh0FImJXz9vtxXdk3KgQQEYglVdma2r5Zz-S2yiLNzA-sxg1OhsGCS1/pub?w=960&h=720″][/vc_column][/vc_row]