[vc_row][vc_column][vc_column_text el_id= »objectif-1″]

Fonctions – modéliser

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Dans $y = f (x)$ , on dit que $y$ s’exprime en fonction de $x$

On peut aussi parfois exprimer $x$ en fonction de $y$

Exemple : La formule $v = \frac{d}{t}$ s’écrit aussi

$d = v \times t$
$t = \frac{d}{v}$

[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

Quizz

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-2″]

Fonctions – calculer

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Une fonction $f$ associe à une valeur $x$ une autre valeur $y$ .

On écrit $y = f (x)$

$y$ est l’image de $x$ par $f$

$x$ est l’antécédent de $y$ par $f$ [/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]

Quizz :

On donne la fonction définie par $f (x) = x^{2} + 3$ . Répondre aux 4 questions suivantes :[/vc_column_text][vc_column_text]

[/vc_column_text][/vc_column][vc_column width= »1/2″][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-3″]

Fonction – graphique

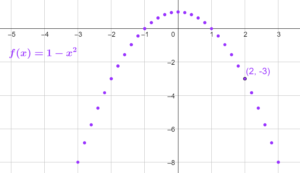
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Dans un graphique, on note en ordonnée ( $y$ ) les image des nombres de l’axe des abscisses ( $x$ ), et on place tous les points de coordonnées ( $x; f (x)$ )

Par exemple, le point de coordonnées $(2; - 3)$ est obtenu en calculant $f (2) = 1 - 2^{2} = - 3$ [/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

Quizz :

On donne la courbe suivante[/vc_column_text][vc_single_image image= »2627″ img_size= »300×200″ alignment= »center » style= »vc_box_rounded » onclick= »kalium_lightbox »][vc_column_text]Répondre aux 4 questions suivantes :[/vc_column_text][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Fonctions – Résolutions graphiques

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprietepremieresthr propriete »]Dans un graphique, on résout l’équation $f (x) = k$ en traçant une droite à la hauteur $k$ et en repérant les points d’intersection avec la courbe.

Les solutions se lisent sur l’axe des abscisses.

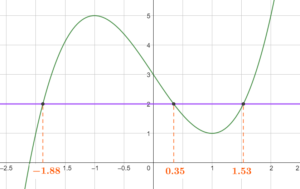
Par exemple, l’équation $f (x) = 2$ admet 3 solutions. Valeurs approchées : -1,88 ; 0,35 ; 1,53[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column width= »1/2″][vc_row_inner][vc_column_inner][vc_column_text]

Quizz :

On donne la courbe suivante[/vc_column_text][vc_single_image image= »2645″ img_size= »300×200″ alignment= »center » style= »vc_box_rounded » onclick= »kalium_lightbox »][vc_column_text]Répondre aux 4 questions suivantes :[/vc_column_text][vc_column_text]

[/vc_column_text][/vc_column_inner][/vc_row_inner][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Plan de travail

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vRayoIydf7RYe4LPzU_CTJwnQdW28aSFetU1SLPCSJ0KMsXr_Rbu1a2bO8f0bZqTEf99tVWadyNK2cg/pub?w=960&h=720″][/vc_column][/vc_row]