Répétition de deux épreuves aléatoires indépendantes
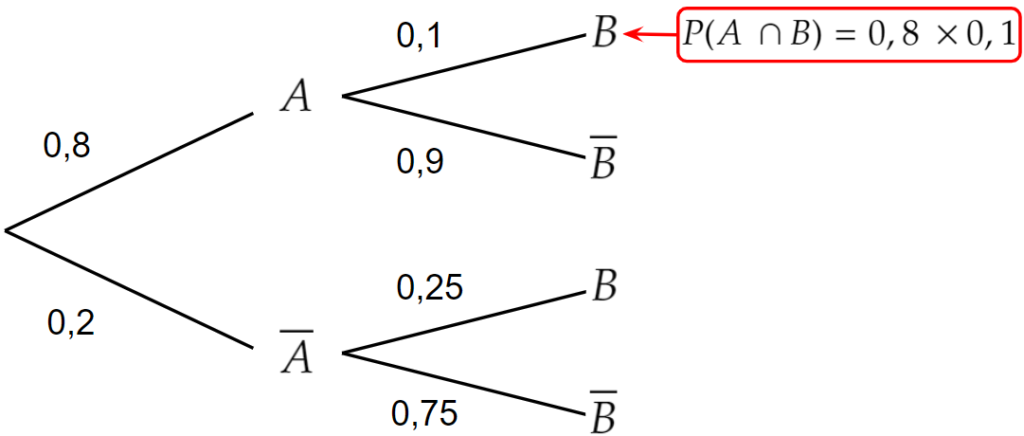
Lors de la répétition de deux épreuves indépendantes, la probabilité \(P ( A \cap B)\) est le produit des probabilités le long des branches passant par \(A \) et par \(B \)
Loi de Bernoulli et variables aléatoires
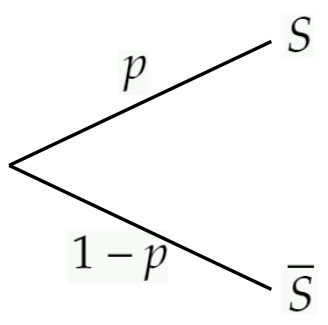
Une épreuve de Bernoulli de paramètre \(p\) donne un succès (\(S\) ) avec une probabilité \(p\) et un échec ( \( \overline{S} \)) avec une probabilité \(1-p\)
Lorsqu’on répète plusieurs expériences de Bernoulli, on peut compter le nombre de succès dans une variable aléatoire \(X\) et calculer la probabilité d’obtenir un nombre \(a\) de succès (on écrit alors \(P(X=a)\))
Loi de probabilité, espérance
La loi de probabilité de \(X\) est l’ensemble des valeurs qu’elle prend associées aux probabilités correspondantes (souvent représentées en tableau)
| \(a\) | \(a_1\) | \(a_2\) | \(a_3\) | … |
| \(P(X=a)\) |
L’espérance de \(X\) est le nombre
\(E(X)=a_1 \times P(X=a_1) + a_2 \times P(X=a_2) + a_3 \times P(X=a_3) \times …\)