[vc_row][vc_column][vc_column_text]

Produit d’un vecteur par un réel

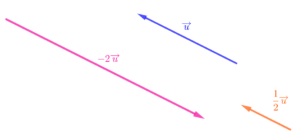
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires lorsqu’il existe un nombre $k$ non nul tel que $\overrightarrow{u}=k\times \overrightarrow{v}$.

Dans ce cas, les vecteurs ont :

• la même direction (mais pas forcément le même sens car cela dépend du signe de $k$ ),
• des longueurs qui vérifient $||\overrightarrow{u}||=|k|\times ||\overrightarrow{v}||$ )

[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]

Quizz

[/vc_column_text][/vc_column][vc_column width= »1/2″][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Alignement et parallélisme

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Si $\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont colinéaires alors les droites $(AB)$ et $(CD)$ sont parallèles.

Si $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires alors les points $A,B,C$ sont alignés.[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Déterminant de deux vecteurs

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Le déterminant de deux vecteurs $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x^{\prime };y^{\prime })$ est le nombre 

$det(\overrightarrow{u},\overrightarrow{v})=x{y}^{\prime }-x^{\prime }y$

[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]

Quizz

[/vc_column_text][/vc_column][vc_column width= »1/2″][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Démonstration

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Lorsque le déterminant de deux vecteurs vaut 0 alors ils sont colinéaires[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Synthèse :

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vS1-16VoV0hv-BsEr8NP_9BhSdlPy2jQndL6hOrFD6jyWnObMElvgUyusQOmr5rXDwn1n4bkU8D-_eA/pub?w=960&h=720″][/vc_column][/vc_row]