[vc_row][vc_column][vc_column_text]
Projeté orthogonal
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Le projeté orthogonal d’un point M sur une droite (d) est le point de (d) le plus proche de M. On le trouve en traçant la perpendiculaire à (d) passant par M.
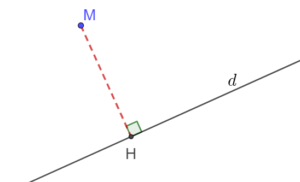 [/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]La médiatrice d’un segment est la droite qui lui est perpendiculaire en son milieu.
Les médiatrices d’un triangle se coupent au centre du cercle circonscrit au triangle
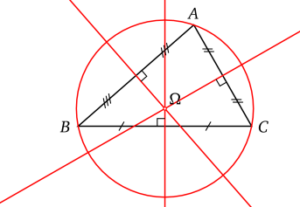 [/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]La hauteur d’un triangle est la droite perpendiculaire à un côté passant par un sommet.
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]La hauteur d’un triangle est la droite perpendiculaire à un côté passant par un sommet.
Le pied de la hauteur est le projeté orthogonal du sommet sur le côté.
Les hauteurs d’un triangle se coupent en un point appelé orthocentre du triangle.
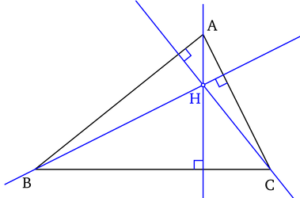
On dit que les hauteurs sont issues de A, de B ou de C[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]
Quizz
Répondre aux trois questions
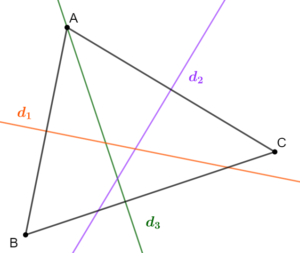
Le triangle rectangle
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Tout point d’un cercle forme avec un diamètre un triangle rectangle.
[BC] est un diamètre donc les triangles BCA et BCD sont rectangles[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]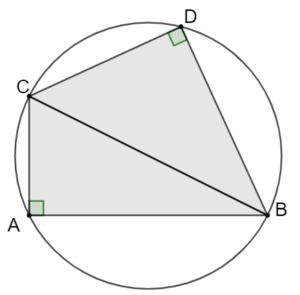 [/vc_column_text][/vc_column][/vc_row][vc_row][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]
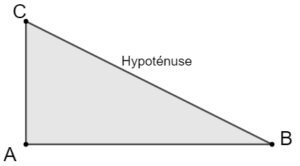
Théorème de Pythagore :
Dans un triangle ABC rectangle en A, on a
AB²+AC² = BC²
 [/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
Pour aller plus loin : La formule d’Al-Kashi :
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_class= »proprieteseconde propriete »]
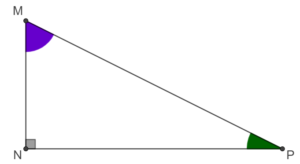
Formules de trigonométrie :
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Quizz
Répondre aux trois questions
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Plan de travail
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vQhdsVJarI_9rNPy5jchXsVP9xZV7J94FrsKerKbRoAHXopicXTpgnX96GH8_aQr7SLMVNWGUMMGosS/pub?w=960&h=720″][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Synthèses :
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vQSFzTA83rzCTxzzixIt9boe2hVSy7rj2wfhClNS6Jnpo9dTVo1mqJwU1cw_CC5Ctv_4DUZFpuVDuEw/pub?w=960&h=720″][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vQIGL8n8uCkxDWEyNudvj6WNFYET4tNwJUY5tmhCy73ZsaZ5z8ZE1PFRhDUToY7Ut4sO_qhWxzWlst1/pub?w=960&h=720″][/vc_column][/vc_row]
