[vc_row][vc_column][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]
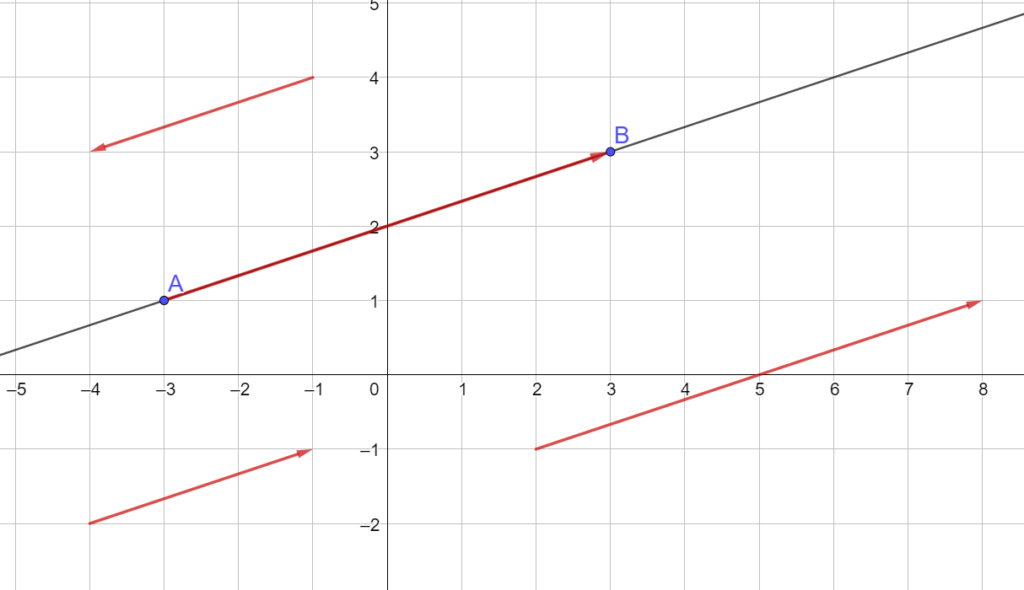
Équation cartésienne et vecteur directeur
[/vc_column_text][vc_column_text el_class= »proprieteseconde propriete »]Une droite dans un repère a pour équation cartésienne
Le vecteur
Si
Si
Si
 [/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
Équation réduite et coefficient directeur
[/vc_column_text][vc_column_text el_class= »proprieteseconde propriete »]Une droite non verticale dans un repère a pour équation réduite
Le nombre
Le nombre
Si
Donc
et
Quizz
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Droites parallèles ou sécantes
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text el_class= »proprieteseconde propriete »]Deux droites d’équations
Dans ce cas pour trouver le point d’intersection on résout le système formé par les deux équations.[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]
Quizz
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Démonstration
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Une équation de droite est de la forme ax + by +c = 0[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Synthèse :
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vSv9SMJbZbBteQ26xBAAAIHSDSJ3gVXOApRLE7RX_fhv0Ec6DbiKNMiq6g4R7hyGuokvz9cVldPVYm8/pub?w=960&h=720″][/vc_column][/vc_row]
