[vc_row][vc_column][vc_column_text]
Fonction carré
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]C’est la fonction qui à \(x\) associe son carré \(x^2\). Sa courbe est une parabole, symétrique par rapport à l’axe des ordonnées (fonction paire).
La fonction carré est décroissante sur \( ]-\infty ; 0]\) et croissante sur \( [0 ; + \infty[\)
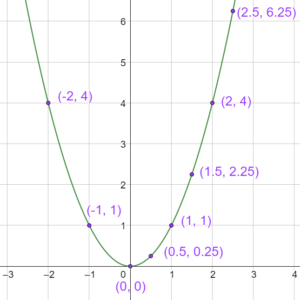[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_images_carousel images= »2980,2981,2982,2983,2984,2985,2986,2987″ img_size= »medium » onclick= »link_no » autoplay= »yes » title= »Trajectoires paraboliques »][vc_column_text]
Quizz
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column width= »1/2″][vc_column_text]Fonction racine carrée
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
Fonction inverse
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]C’est la fonction qui à \(x\) associe sa racine carrée \(\sqrt{x}\).
La fonction racine carrée est croissante sur \( [0 ; + \infty[\)
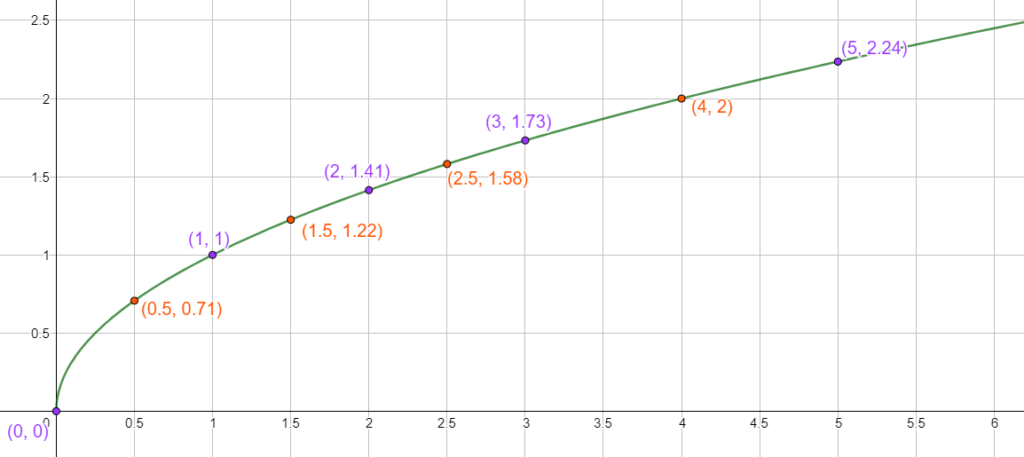[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]C’est la fonction qui à \(x\) associe son inverse \(\frac{1}{x}\). Sa courbe est une hyperbole, symétrique par rapport à l’origine du repère (fonction impaire).
La fonction inverse est décroissante sur \( ]-\infty ; 0[\) et sur \( ]0 ; + \infty[\)
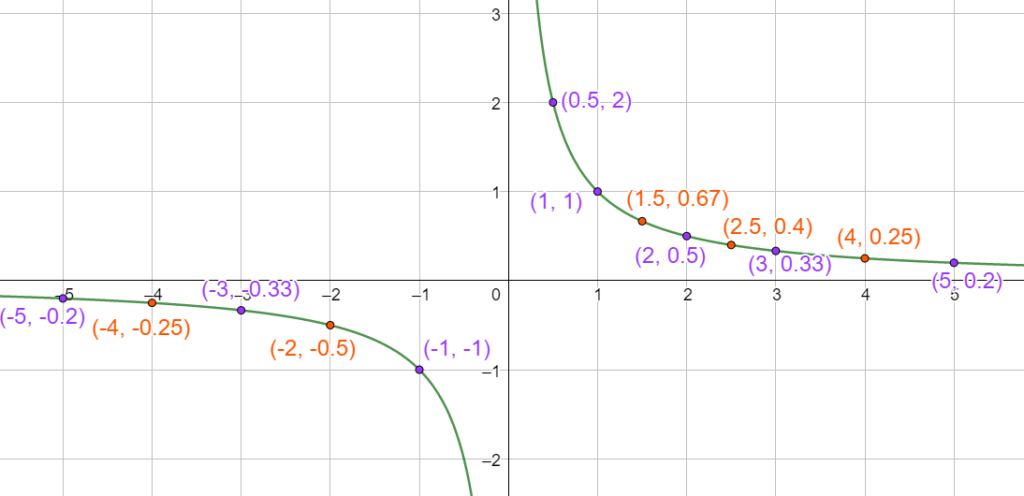[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column width= »1/2″][vc_column_text]
Fonction cube
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
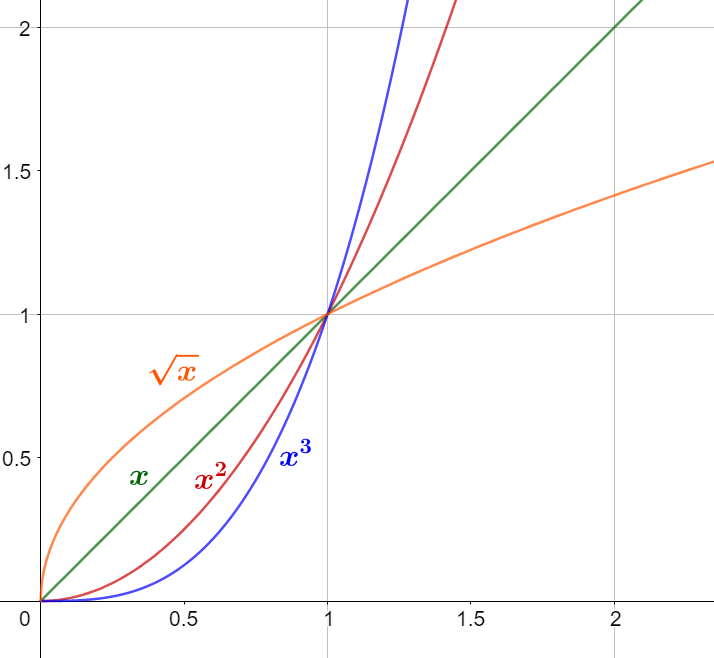
Comparaison
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]C’est la fonction qui à \(x\) associe son cube \(x^3\). Sa courbe est symétrique par rapport à l’origine du repère (fonction impaire).
La fonction cube est croissante sur \( \mathbb{R} \text{ ( sur }]-\infty ; + \infty[ \text{ )}\)
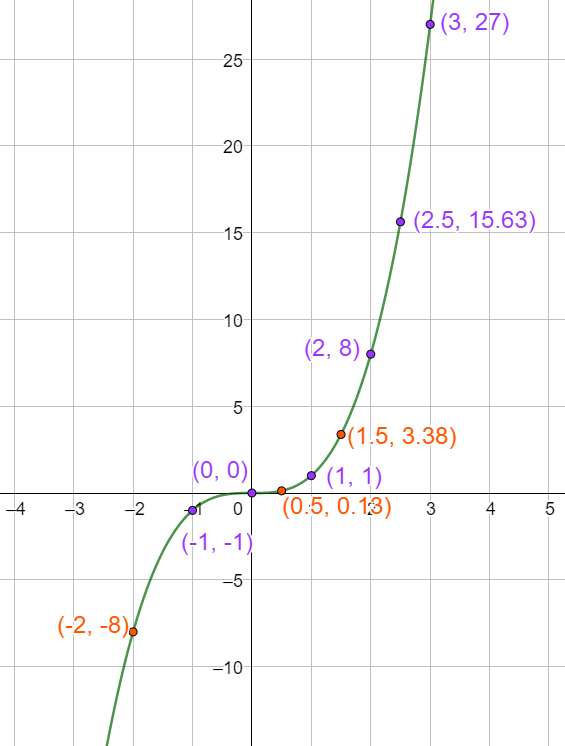[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Pour tout \(x \) de l’intervalle \( ]0 ; 1 [\), on a
\(x^3 < x^2 < x < \sqrt{x}\)
Pour tout \(x \) de l’intervalle \( ]1 ; +\infty [\), on a
\( \sqrt{x} < x < x^2 < x^3\)
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column][vc_column_text]
Quizz
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Démonstration
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]La fonction carré est décroissante sur \( ]-\infty ; 0]\) et croissante sur \( [0 ; + \infty[\)[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Synthèse :
[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vT7w-RI1W8N1x6J64WyK40h60EM9MQ7TgDq6CugYDIQ5FRHKtEdiiHEOU6vOxRoC0_-6bAJlitEd4_i/pub?w=960&h=720″][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vQjLhQjHJczqjS3fXurqfbWbdhxxCnhru0-3Ru9zpOvM6GI5EHNwivAmmEvfyrOGbUe07gao4hJ5eYc/pub?w=960&h=720″][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vRKi0qWJ5dhSQdmCmvAEJa8XqR8wKFoJ7Ba7A7P3wDs-NiRc9lrrYeWvxfSsJnOEMahnj9M8S_FVaJ9/pub?w=960&h=720″][/vc_column][/vc_row]