[vc_row][vc_column][vc_column_text el_id= »objectif-1″]

Définitions

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Expérience : Exemple : « On lance deux dés et on note la somme de leurs face. »

Univers : l’ensemble de toutes les sommes possibles : {2 ; 3 ; 4 ; … ; 12} (11 éléments)

Issue : L’un des éléments de l’univers

Événement : Exemple : A : « La somme obtenue est un multiple de 3 », c’est l’ensemble {3 ; 6 ; 9 ; 12} (4 éléments)

Probabilité : C’est le nombre \(P(A)=\displaystyle \frac{\text{Nombre d’éléments de A}}{\text{Nombres d’éléments de l’univers}}=\frac{4}{11}\)

Événement contraire, noté \(\overline{A}\) : ce sont les éléments qui n’appartiennent pas à A. On a \(P(\overline{A})=1-P(A)\).[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Réunion : noté \(A \cup B\) ; c’est l’ensemble des éléments appartenant à A ou à B (ou aux deux).

Intersection : noté \(A \cap B\) ; c’est l’ensemble des éléments appartenant en même temps à A et à B.

Formule : \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)

(s’écrit aussi \(P(A \cap B)+P(A \cup B)=P(A)+P(B)\) )[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]

Quizz

[/vc_column_text][/vc_column][vc_column width= »1/2″][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-3″]

Tableaux et arbres

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Exemple de répartition des élèves dans une classe :

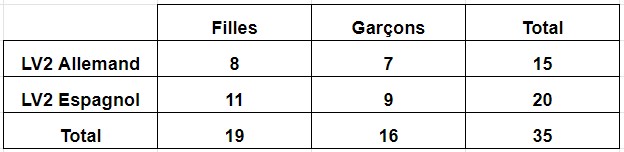[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Arbre de probabilités correspondant :

(F : « l’élève est une fille » et E : « l’élève fait LV2 Espagnol »)

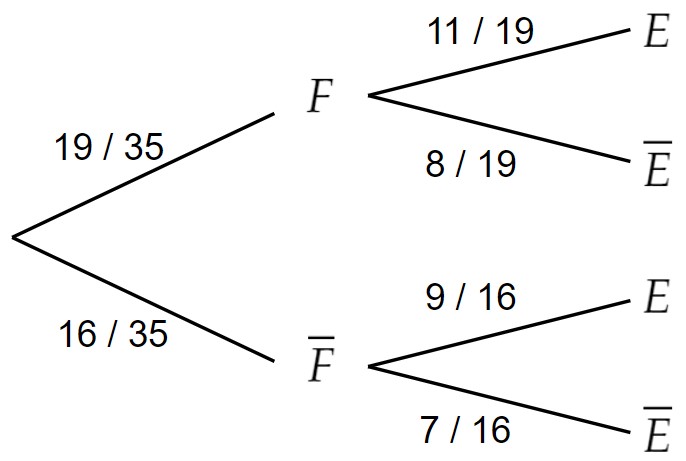[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Échantillonnage

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Lorsqu’on répète un grand nombre N de fois une expérience, dans laquelle on note p la probabilité d’un événement A, alors la fréquence de réalisation de A est plus de 95 % du temps dans l’intervalle \(\displaystyle \left[p-\frac{1}{\sqrt{N}} ; p+\frac{1}{\sqrt{N}}\right]\)[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Synthèse :

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vSnNUmCjTnUY3zm1r6UUk1AMQTQMO4jy2BYon2XlZmIHqmhXTnheqz5ZEiiN3OCk1Dof-UWIc_y0zjy/pub?w=960&h=720″][/vc_column][/vc_row]