01 – La clôture
Jean possède une clôture de 75 mètres de long pour protéger ses poules. L’enclos doit être rectangulaire et le plus spacieux possible.
Comment doit-il faire ?
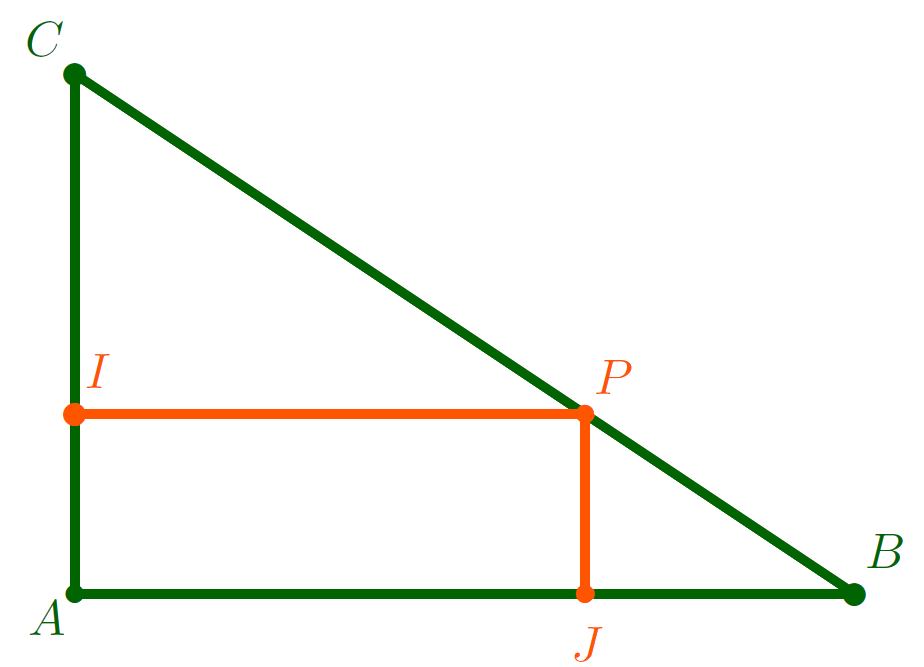
02 – Dans un triangle
$ABC$ est un triangle rectangle en $A$
tel que $AB=6$ cm et $AC=4$ cm.
Où faut-il placer $P$ sur l’hypoténuse pour que la longueur $IJ$ soit la plus petite possible ? Justifier.
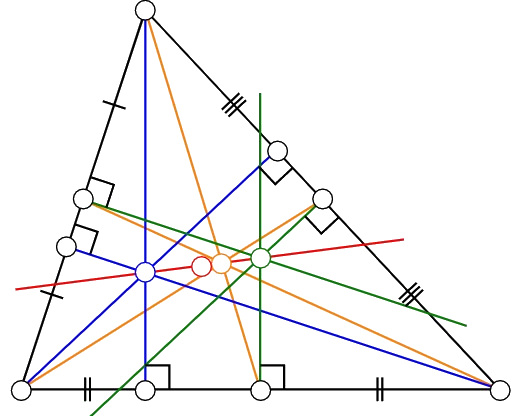
03 – Triangle remarquable autour des droites
- Étant données trois droites concourantes $(d_1)$, $(d_2)$ et $(d_3)$, tracer un triangle $ABC$ dont elles sont les hauteurs.
- Étant données trois droites concourantes $(\Delta_1)$, $(\Delta_2)$ et $(\Delta_3)$, tracer un triangle $RST$ dont elles sont les médianes.
04 – Têtes et pattes
Dans la cour d’une ferme, il y a des poules et des lapins. J’ai pu compter 91 têtes et 324 pattes.
Combien y a-t-il de poules et de lapins ?
05 – Vrai spectacle de fauconnerie
Deux faucons sont installés sur des tours distantes de 70 m, l’un à 35 m de hauteur et l’autre à 45 m. Un fauconnier doit les réceptionner au sol entre les deux tours. Les rapaces plongeront en même temps et voleront à la même vitesse en ligne droite.
Où le fauconnier doit-il se placer afin que les oiseaux arrivent au même instant ?
06 – Sous la corde
Une corde non élastique de 101 mètres est attachée au sol entre deux piquets distants de 100 mètres.
En tirant la corde en son milieu et en la levant aussi haut que tu le peux, parviendras-tu à passer en dessous sans te baisser ?
07 – La course à 20
Ratchet propose à Clank de jouer avec lui à la course à 20…
Il commence en écrivant au choix 1 ou 2.
Clank ajoute 1 ou 2 au nombre de Ratchet.
Ratchet, à son tour, ajoute 1 ou 2 au nombre de Clank.
Et ainsi de suite, chacun à tour de rôle !
Ratchet a vite trouvé une stratégie pour gagner à chaque fois.
Trouve et explique à Clank sa stratégie !
08 – Bicarré
Construire sans mesurer deux carrés de sorte que le deuxième ait une aire qui vaut exactement le double de celle du premier.
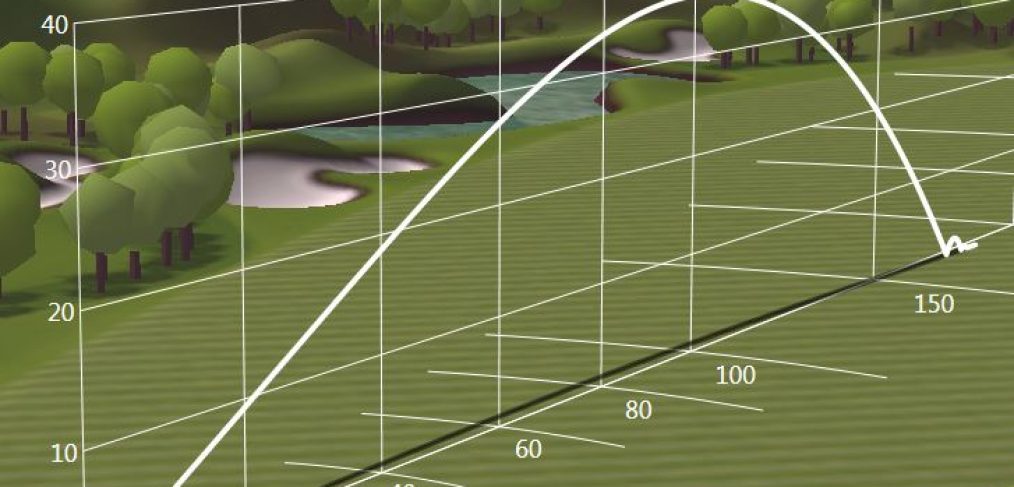
09 – Sans question, cent questions !
La trajectoire d’une balle dans l’air est donnée par :
$$f(x)=\dfrac{150x – x^2}{145}$$
où $x$ est le temps écoulé depuis le lancer, exprimé en secondes, et $f(x)$ la hauteur de l’objet à l’instant $x$, exprimée en mètres.
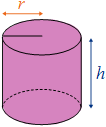
10 – Le bidon
On considère un cylindre de hauteur $h$ et dont la base a pour rayon $r$ (en dm). Ce cylindre doit contenir 5 Litres.
Quelles sont les possibilités ?
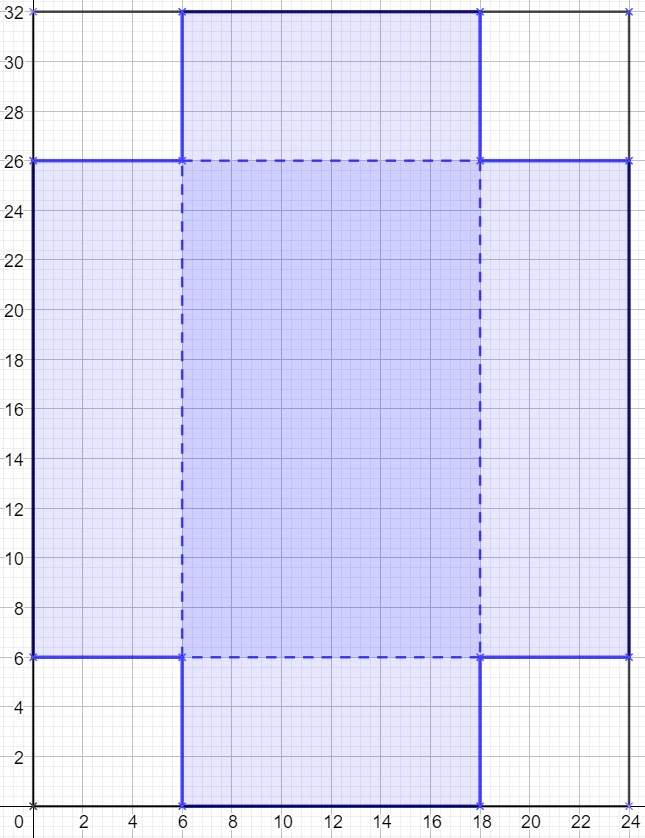
11 – C’est dans la boîte, Patron !
Voici le patron d’une boite sans couvercle découpé dans une feuille cartonnée de dimensions 24 x 32 (en cm).
Objectif : Déterminer les dimensions de la boite ayant le plus grand volume.
Vous expliquerez précisément le raisonnement utilisé
12 – Plus tu montes, moins ça compte
Un astronaute pèse $m$ kg sur Terre au niveau de la mer, sa masse apparente (en kg) à l’altitude $h$ (en km) au-dessus du niveau de la mer est donné par :
$$M= m \times \left(\dfrac{6400}{6400+h}\right)^2$$
L’astronaute pèse 70 kg au niveau de la mer.
À quelle hauteur pèsera-t-il moins de 2kg ?
13 – Quel rectangle ?
Un rectangle a un périmètre de 110 m et une aire de 714 m².
Déterminer les mesures de ses côtés.
Bonus : Trouvez le lien avec l’image ci-contre …
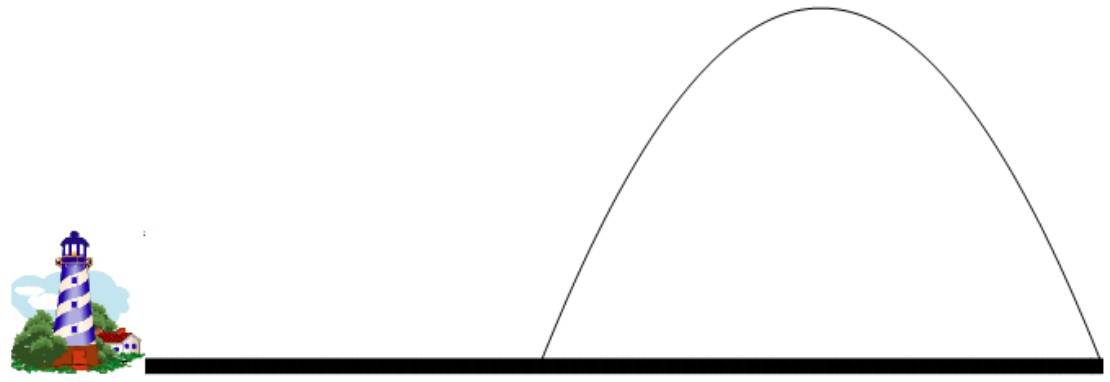
14 – Le phare
Un phare de hauteur 20m est situé à 700m du pied d’une colline. La colline culmine à 500m, sa base mesure 1000m, et on suppose qu’ elle a une forme parabolique.
Quelle est l’altitude du point de la colline le plus élevé que peut éclairer le phare ?
15 – Cote, cote
Un fermier décide de réaliser un espace poulailler rectangulaire le long du mur de sa maison (un côté mur et trois côtés clôture). Il veut offrir à ses poules 300 m$^2$ d’espace.
Comment peut-il placer les piquets pour que la longueur de clôture à acheter soit minimale ?
16 – Objectif : doubler
Une école de commerce vient d’ouvrir et compte 600 étudiants scolarisés. Elle évalue à 7 \% par an la progression de ses effectifs et se fixe comme objectif de les doubler avant 10 ans.
Qu’en pensez-vous ?
17 – Le problème d’Erdős
Problème posé par Erdős au jeune mathématicien Lajos Pòsa au début d’un dîner :
« Étant donné l’ensemble des entiers de 1 à $2n$, et l’un de ses sous ensemble $A$ contenant $n+1$ éléments. Y a-t-il toujours deux éléments de $A$ dont l’un divise l’autre ? »
- Au dessert, Lajos avait la solution… et vous ?
- Présenter une recherche documentée sur le mathématicien Erdõs en quelques lignes. En particulier, on pourra consulter Tangente n°152.
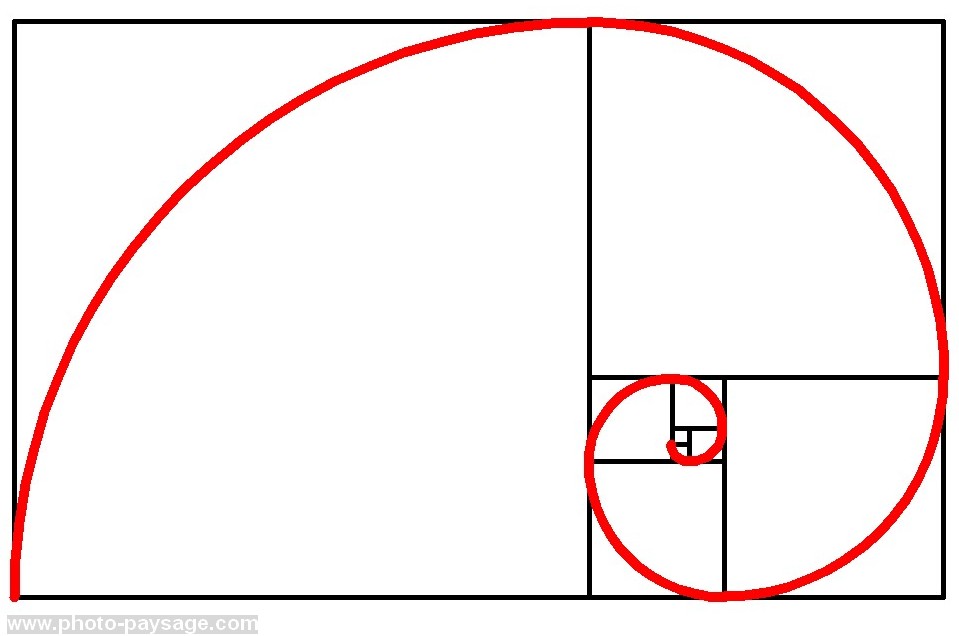
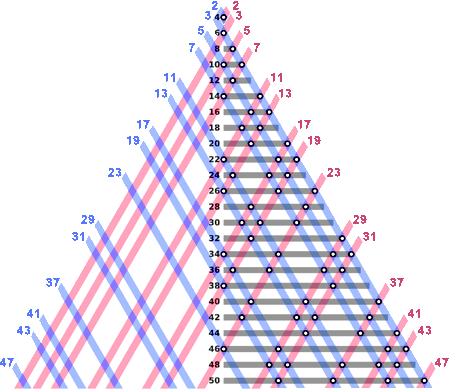
18 – La conjecture de Goldbach
«Tout nombre pair est la somme de deux nombres premiers.»
Formulée en 1742 par Christian Goldbach, c’est l’un des plus vieux problèmes non résolus de la théorie des nombres et des mathématiques.
- À l’aide de la figure ci-contre, vérifier cette conjecture pour tous les nombres entiers inférieurs à 30.
- Exposer une recherche documentée de quelques lignes sur cette conjecture.
19 – Marabout de ficelle
On coupe une ficelle de 32 cm de long en deux morceaux avec lesquels on forme un carré et un triangle équilatéral.
Où doit-on couper la ficelle pour que l’aire totale soit la plus petite possible ?
20 – Date d’anniversaire
Chloé rencontre Alexis et Benoît en vacances et leur fait deviner sa date d’anniversaire. Elle donne dix dates possibles.
Facétieuse et bonne logicienne, elle donne le mois à Alexis et le jour à Benoît.
Les deux amis tiennent alors cette conversation :
Alexis : «Je ne connais pas la date anniversaire de Chloé, mais je sais que tu ne la connais pas non plus.»
Benoît : «Effectivement je ne la connaissais pas mais grâce à toi, je la connais maintenant.»
Alexis : «Alors moi aussi, je la connais !»
Quelle est la date de naissance de Chloé ?
21 – Jeu de hasard
- On joue à un jeu de hasard où on gagne une fois sur 10.
Johann affirme : « Donc si on joue 5 fois de suite, on a logiquement une chance sur deux de gagner ».
Discuter cette affirmation. - Généralisation : Un jeu est gagnant avec une probabilité $p=\dfrac{1}{2n}$. On joue $n$ fois.
Exprimer en fonction de $n$ la probabilité de gagner.
22 – Dilatation de matériaux
Lorsqu’un matériau de longueur $L$ subit une variation de température $\Delta T$, ses dimensions varient proportionnellement à la variation de température : $$\dfrac{\Delta L}{L}=\alpha \Delta T$$
où $\alpha$ est le coefficient de dilatation propre à chaque matériau (voir tableau)
- Une tige de cuivre mesure 3m à 25°C.
Quelle est sa taille si on la chauffe à 60°C ? - À quelle température devrait-on chauffer cette tige pour que sa longueur augmente de 1 cm ?
23 – Proportion d’étudiants
Un groupe d’amis, dont certains ont une carte « Avant’âge », va au cinéma. Le prix d’une place est de 4 € pour les détenteurs de la carte et de 6 € pour les autres. Pour le groupe, le prix total des places est de 52 €.
Ce même groupe assiste quelques jours plus tard à un concert. Le prix d’une place est de 18 € pour ceux qui ont la carte et de 30 € pour les autres. Pour le groupe, le prix total des places est de 240 €.
En détaillant précisément votre démarche, trouver la proportion de carte « Avant’âge » dans le groupe.
24 – Alignement
$ABCD$ est un rectangle de longueur 6 et de largeur 4. $M$ est un point du segment $[BD]$, $N$ est le symétrique de $C$ par rapport à $M$.
La parallèle à $(AD)$ menée par $N$ coupe $(AB)$ en $P$.
La parallèle à $(AB)$ menée par $N$ coupe $(AD)$ en $Q$.
En détaillant précisément votre démarche, déterminer si les points $M$, $P$ et $Q$ sont alignés.
25 – Histoire d’angles
Soient huit carrés identiques.
Combien mesure $a+b+c$ ?
26 – Engage le jeu que je le gagne
- Décrire cette pyramide.
- Trouver deux nombres premiers palindromes à 4 chiffres.
- Trouver tous les nombres premiers palindromes à 4 chiffres.
- (Facultatif) Écrire un programme qui génère les nombres premiers palindromes à $n$ chiffres.
27 – Comme nos aïeux
Le document suivant est extrait d’une table de logarithme (« Nouvelles table de logarithme, édition 1911 »).
En effectuant une seule addition, calculez le produit $35 \times 27$.
En effectuant une seule soustraction, calculez le quotient $\dfrac{779}{19}$
28 – Ah toi aussi ?!
Dans une classe de 27 élèves, quelle est la probabilité qu’au moins deux d’entre eux aient la même date d’anniversaire ?
Combien faut-il d’élèves dans la classe pour que cette probabilité dépasse les 95 % ?
29 – Efficacité d’un test
Une maladie est présente dans la population, avec la proportion d’une personne malade sur 10 000. Le responsable d’un laboratoire pharmaceutique souhaite faire approuver un nouveau test de dépistage qui vérifie que, si une personne est malade, alors le test est positif à 99 %, et que, si une personne n’est pas malade, alors le test est positif à 0,1 %.
Pour savoir si le laboratoire peut commercialiser son test,on souhaite connaître la probabilité qu’une personne soit malade si le test est positif.
30 – Il n’y a pas que le bluf dans la vie
On assiste à une partie de poker (Texas Hold’em).
Observez cette image et discuter les probabilités affichées en pourcentages.
31 – Le Chevalier de Méré
Le problème suivant, soumis par le Chevalier de Méré à Pascal en 1654, est l’un de ceux qui marque le début de l’étude des probabilités dans l’histoire.
« Est-il avantageux, lorsqu’on joue au dé, de parier sur l’apparition d’un 6 en lançant 4 fois le dé?»
«Est-il avantageux de parier sur l’apparition d’un double-six, quand on lance 24 fois deux dés ?»
Discutez le sens de ce questionnement et apportez-y votre solution.
32 – Croix et Pile ou Face
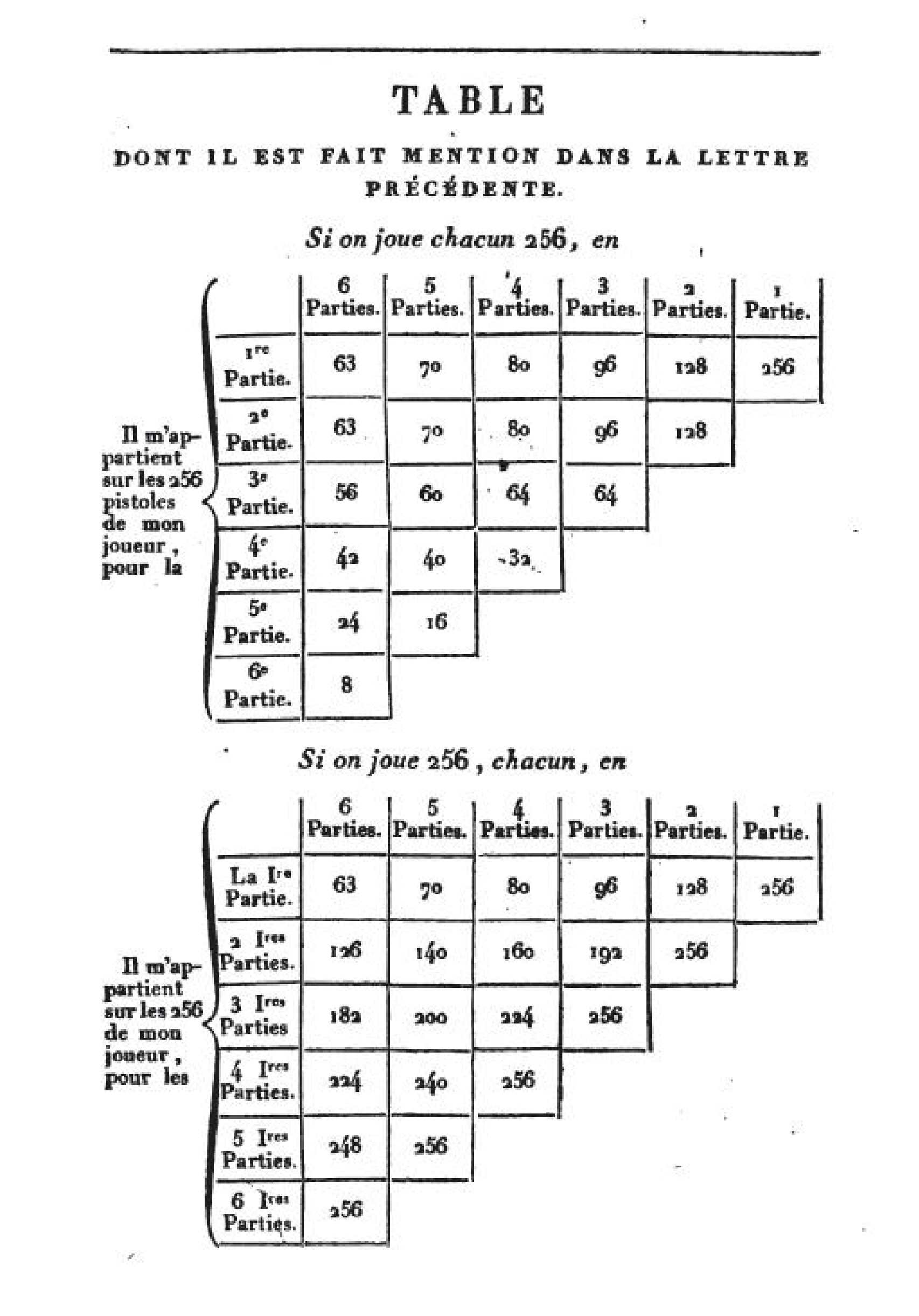
Problème exposé par Blaise Pascal en 1654 à Pierre de Fermat.
«Pierre et Blaise misent chacun 32 pistoles et jouent à croix et pile (Pile ou Face).
Pierre mise sur « croix », Blaise mise sur « pile ». Le jeu s’interrompt dès qu’on a obtenu 3 fois « croix » ou 3 fois « pile ».
Le gagnant empoche alors les 64 pistoles.
La pièce a été lancée une fois et elle est tombée sur « croix ».
Pour une raison quelconque, le jeu doit s’interrompre brutalement.
Comment répartir équitablement les 64 pistoles entre les deux joueurs ?»
33 – Gratter c’est gagner
La JdJ (Jurassienne des Jeux) a noué un partenariat avec les Sorciers de la Côte pour un nouveau jeu à gratter.
L’équipe commerciale s’interroge sur le prix du ticket.
34 – Phileas Fogg
Combien de temps mettriez vous en marchant au-dessus de l’équateur pour faire le tour de la Terre ?
35 – Plus haut, toujours plus haut…
On imagine posséder une feuille de papier que l’on peut plier indéfiniment. Elle a une épaisseur de 0,5 mm.
On l’a déjà pliée en deux suffisamment de fois pour atteindre le Mont Blanc.
Combien de pliures nous reste-t-il a effectuer pour arriver jusqu’à la Lune ? Jusqu’au Soleil ?
36 – Tour du monde à la corde
On imagine posséder une corde (non extensible) que l’on a tendue tout autour de l’équateur.
Quelle serait la longueur du morceau de corde à ajouter pour que la corde se retrouve à 1 m du sol partout autour de la Terre ?
37 – C’est quoi ce rectangle ?!
Un rectangle a un périmètre de 17 cm et une aire de 17 cm².
Quelles sont ses dimensions ?
38 – Boulindrosphère
«Un cylindre qui a une base égale à un grand cercle d’une sphère, et une hauteur égale au diamètre de cette sphère, est égal à trois fois la moitié de cette sphère, et la surface de ce cylindre est aussi égale à trois fois la moitié de la surface de cette même sphère.»
Expliquez et démontrez cette découverte d’Archimède vers 220 Av. J.-C.
39 – Bain de boule
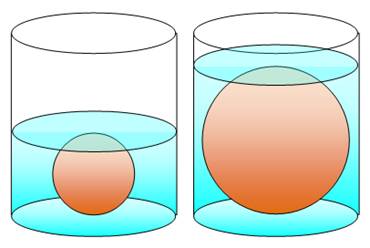
Une boule en acier de rayon 5 cm est placée dans un cylindre de rayon 10 cm et de hauteur 22 cm. On verse du liquide jusqu’à recouvrir exactement la boule (assez lourde pour rester au fond). On retire la boule tout en conservant le liquide.
Existe-t-il un autre format de boule qui, plongée dans le liquide, serait à son tour exactement recouverte par l’eau comme la première ?
40 – La suite de Fibonacci
La suite de Fibonnacci est la suite de nombres dont «chaque terme est la somme des deux précédents» :
0 ; 1 ; 1 ; 2 ; 3 ; 5 ; 8 ; 13 ; 21 …
Écrire un programme qui génère la suite de Fibonnacci puis qui calcule le quotient de deux termes consécutifs $\left(\dfrac{5}{3} ; \, \dfrac{8}{5} ; \, \dfrac{13}{8} ; \, \text{ etc.} \right)$
Que remarque-t-on ?
41 – Polygone inscrit
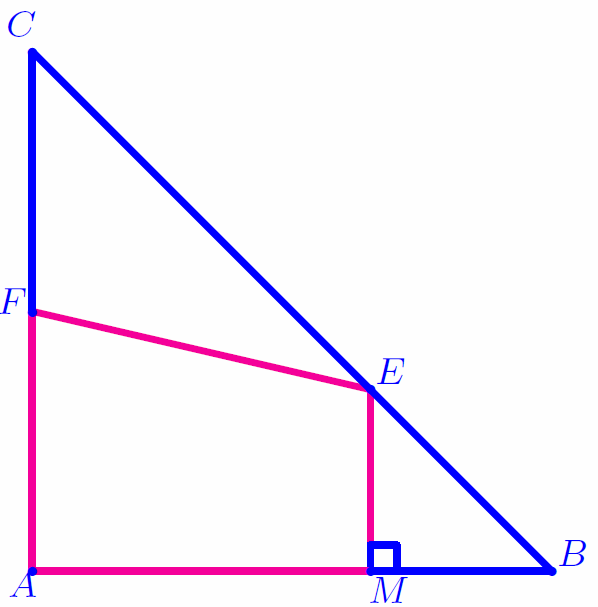
On considère un triangle ABC isocèle et rectangle en A tel que AB=5 cm.
Soit F le milieu de [AC] et M un point de [AB]. Soit (d) la perpendiculaire à (AB) issue de M, elle coupe (BC) en E.
On s’intéresse à l’aire du polygone EFAM.
Le but de la recherche est de trouver la position du point M sur [AB] pour laquelle l’aire est maximale.
42 – Code secret
Dans le coffre de Math Leriche, le code d’ouverture est un nombre à 4 chiffres.
Si tu diminue le code de 12 % puis doubles le résultat, tu obtiens le même nombre que si tu augmentes le code de 28 %, puis ajoute 972.
Quel est le code d’ouverture du coffre ?
43 – La guerre des prix
Sophie veut acheter un ordinateur. Deux magasins vendent le même produit, avec un prix de vente identique. Chacun propose une promotion.
Dans le magasin A, on lui propose une réduction de 10 % sur le prix public, mais elle doit payer en plus 2 % du montant de sa facture pour la livraison et l’installation.
Dans le magasin B, on lui propose simplement une réduction de 8 %.
Quelle est la solution la plus avantageuse pour Sophie ?
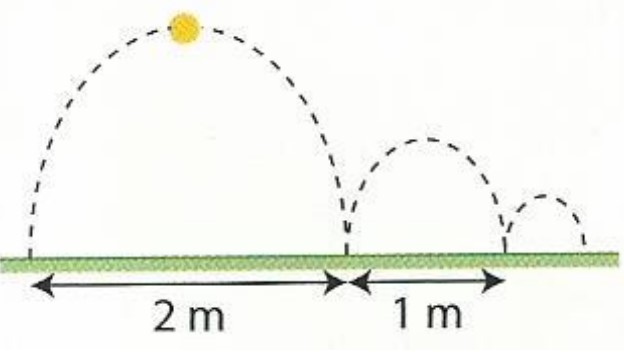
44 – Re-bonds
On lance une balle comme ci-contre.
Elle rebondit en avançant chaque fois d’une longueur égale à la moitié de la précédente. Son premier rebond l’a fait avancer de 2 m.
Quelle sera la distance parcourue après 7 rebonds ? 70 rebonds ?
45 – $\pi=2$
Sur un segment de longueur 2 cm, on considère la suite de lignes $\mathscr{L}_n$ suivante : On commence avec $\mathscr{L}_1$ le demi-cercle de rayon 1 cm, puis on construit $\mathscr{L}_2$ avec 2 demi-cercles de rayon 0,5 cm, puis $\mathscr{L}_3$ constituée de 4 demi-cercles de rayon 0,25 cm, et on continue ainsi de suite comme sur la figure ci-contre.
Étudier la longueur de $\mathscr{L}_n$ pour $n$ de plus en plus grand.
46 – Géométrie du triangle : La relation de Sylvester
Soit $O$ le centre du cercle circonscrit à un triangle $ABC$ et $H$ son orthocentre.
Alors $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$.
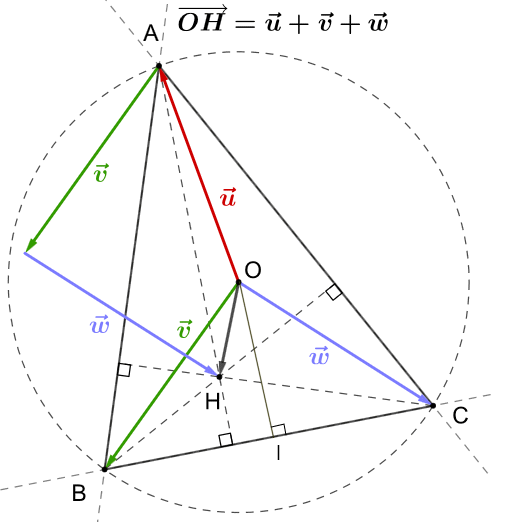
47 – Géométrie du triangle : Relation vectorielle du centre de gravité
Illustrer et démontrer la propriété suivante :
Soit $G$ le centre de gravité d’un triangle $ABC$.
Alors $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.
48 – Géométrie du triangle : La droite d’Euler
Illustrer dans une figure codée puis démontrer la propriété suivante (on peut utiliser la relation de Sylvester du pb n°46) :
Soit $O$ le centre du cercle circonscrit à un triangle $ABC$, $G$ son centre de gravité et $H$ son orthocentre.
Alors $O,G$ et $H$ sont sur une droite appelée la droite d’Euler du triangle.
49 – Au moins un
Environ 42 % des français sont du groupe sanguin O (donneur universel). On étudie le groupe sanguin de quatre personnes prises au hasard dans la population française.
Quelle est la probabilité qu’au moins l’une d’entre elles soit du groupe O ?
50 – Optimiser
Des lycéens réalisent un fanzine.
Lorsque le journal est vendu 1,50 €, ils vendent 400 exemplaires de chaque numéro. Ils ont remarqué que chaque hausse de 10 cts du journal fait perdre en moyenne 8 lecteurs (et inversement, chaque baisse de 10 centimes en fait gagner 8).
Quel serait le prix de vente optimal du journal ?
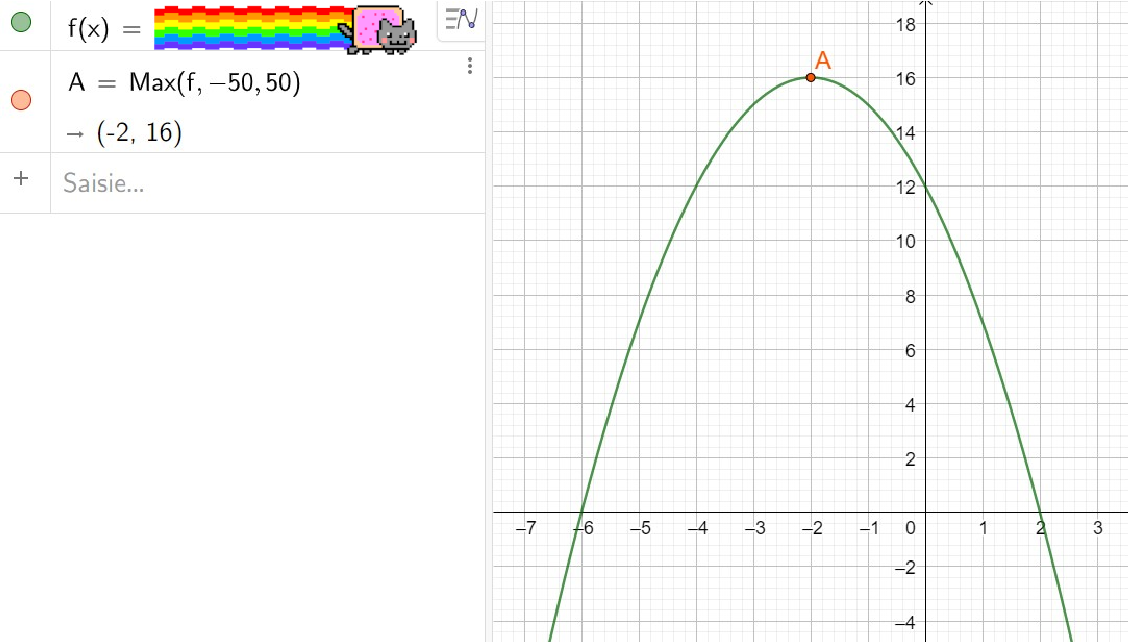
51 – Les 3 formes
Déterminer la forme développée, factorisée et canonique de la fonction représentée ici.
52 – Somme et produit
Déterminer deux nombres dont la somme vaut 23 et le produit vaut -1200
Déterminer deux nombres dont la somme vaut 22 et le produit vaut -1200
53 – Équidistances et courbe
Un bateau arrive à proximité de la côte en suivant un phare placé sur un rocher en mer.
Décrire la trajectoire du navire sachant que le capitaine reste toujours à la même distance de la terre et du phare.
54 – Une famille de rectangles
Déterminer tous les rectangles qui ont une aire en cm² égale à leur périmètre en cm.
55 – Taille des joueurs
Vous êtes journaliste sportif, commentez ce graphique.
56 – Tremblez, bourgeois !
Expliquez le message taggé
57 – Ma chère (?) piscine
J’ai une petite piscine, hexagonale, juste ce qu’il faut pour faire trempette l’été, c’est agréable. J’ai voulu savoir combien ça me coûtait de la remplir.
Alors j’ai mesuré l’intérieur d’un des côtés et j’ai trouvé 1m70. La hauteur d’eau nécessaire : 1m20.
Puis je suis allé chercher sur internet le prix de l’eau à Lons le Saunier, j’ai trouvé ce tarif-là :
1,59 €/m3
58 – Les trois phares
Sur la côte, il y a trois phares:
Le premier s’allume pendant 3 secondes, puis s’éteint pendant 3 secondes.
Le deuxième s’allume pendant 4 secondes, puis s’éteint pendant 4 secondes.
Le troisième s’allume pendant 5 secondes, puis s’éteint pendant 5 secondes.
Les trois lumières viennent de s’allumer ensemble.
À quel moment peut-on déterminer la première fois que les trois lumières s’éteignent en même temps ?
À quel moment peut-on déterminer la prochaine fois que les trois lumières s’allumeront en même temps ?
59 – Cube moyen ou moyenne des cubes ?
Une entreprise fabrique sur commande des cubes creux de tailles différentes. En début de processus de fabrication, on détermine la longueur des côtés des cubes à fabriquer et en fin de processus, on détermine leur capacité. Pour avoir une idée de la production, la direction a demandé de procéder à plusieurs mesures sur 500 cubes. Ainsi, la moyenne de leurs côtés est de 10,5 cm et celle de leur volume est 2240 cm3. Voulant tenir compte de toutes les mesures, la direction a conclu que le cube moyen fabriqué par cette entreprise était un cube de côté 10,5 cm et de volume 2240 cm3 !
| Côté | 1 | 5 | 10 | 15 | 20 |
| Volume | 1 | 125 | 1000 | 3375 | 8000 |
| Effectifs | 50 | 120 | 140 | 120 | 70 |
60 – Joyeuses Pâques !
A l’approche des fêtes de Pâques, un artisan chocolatier décide de confectionner des œufs en chocolat. En allant inspecter ses réserves, il constate qu’il lui reste 18 kg de cacao, 8 kg de noisettes et 14 litres (kg) de lait. Il a deux spécialités : l’œuf Extra et l’œuf Sublime.
Un œuf Extra nécessite 100 g de cacao, 100 g de noisettes et 200 ml (g) de lait.
Un œuf Sublime nécessite 300 g de cacao, 100 g de noisettes et 100 ml (g) de lait.
Il fera un profit de 2€ en vendant un œuf Extra, et de 3€ en vendant un œuf Sublime.
Combien d’œufs Extra et Sublime doit-il fabriquer pour faire le plus grand bénéfice possible ?
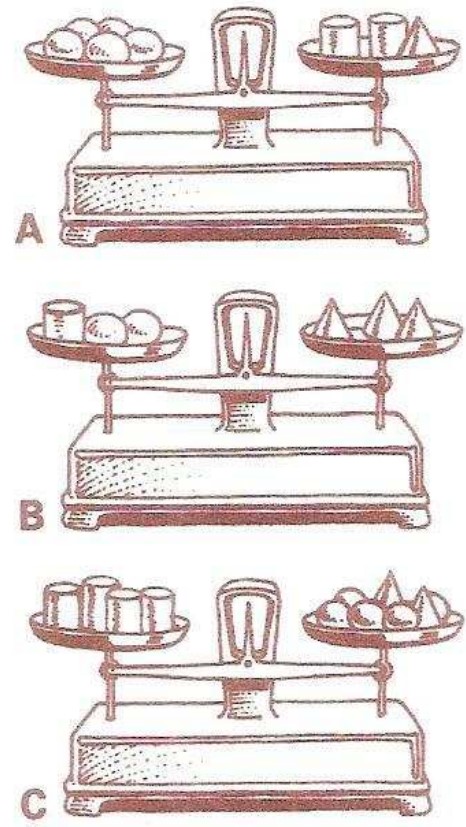
61 – Énigme des balances
Les balances A et B sont en équilibre.
Et la balance C ? Sinon, de quel côté penche-t-elle ?
62 – Ah ça ira, ça ira… à l’heure ?
Voici une horloge révolutionnaire (1 jour dure 10 heures, une heure dure 100 minutes et 1 minute dure 100 secondes).
Quelle heure serait indiquée au même moment sur une horloge classique ?
63 – Pyramide et tronc
À quelle hauteur doit-on couper une pyramide régulière (la hauteur a la même mesure que le côté du carré de base) pour obtenir deux morceaux de même volume ?
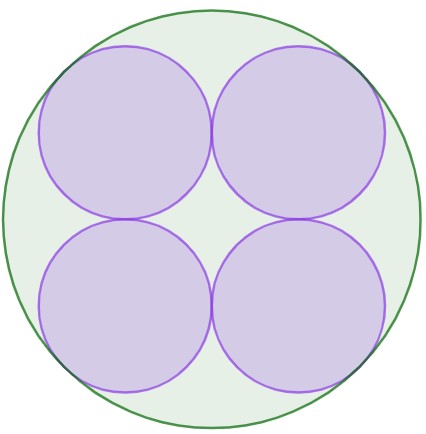
64 – Quatre cercles en un
Dans un grand cercle de rayon 10 cm on construit quatre petits cercles identiques tangents entre eux et au grand cercle.
Quel est le rayon de chacun des quatre petits cercles ?
65 – 4/4 2 P1/2
Dans l’image ci-contre, j’ai coupé ma tranche de pain de mie grillé en quatre parts identiques de deux manière différentes : des parts carrées et des parts triangulaires.
Quelle part a le plus grand périmètre ? La carrée ou la triangulaire ?
Existe-t-il une manière de couper ma tranche en quatre parts identiques pour obtenir un périmètre de part maximal ?
66 – Rationnel ?
67 – Racine carréééééééé…..
Combien vaut $\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\dots}}}}$ ?
