Lors d’une expérience aléatoire, on associe un événement à une quantité (par exemple un gain). La variable X qui représente cette quantité est appelée variable aléatoire.
La probabilité que la variable aléatoire prenne la valeur a s’écrit P(X=a)
Exemple
On lance un dé à 20 faces.
- Si on fait entre 1 et 10, on marque 5 points ;
- si on fait entre 11 et 17 on marque 10 points ;
- si on fait 18 ou plus, on marque 15 points.
On note X la variable aléatoire qui compte le nombre de points marqués.
Le tableau suivant s’appelle al loi de probabilité de X
| a | 5 | 10 | 15 |
| P(X=a) | 0,5 | 0,35 | 0,15 |
Espérance d’une v.a.
Formule (\(a_1, a_2, \dots , a_n \) sont les différentes valeurs prises par X)
\(E(X)=a_1 \times P(X=a_1) + a_2 \times P(X=a_2) + \dots + a_n \times P(X=a_n)\)
Dans l’exemple précédent, l’espérance vaut
\(E(X)=5 \times 0,5 + 10 \times 0,35 + 15 \times 0,15 = 10,375\)
Cela signifie que sur un grand nombre d’essais, on marque en moyenne 10,375 points par lancer.
Loi binomiale
Coefficient binomial
Le coefficient binomial \(\displaystyle {n \choose k}\) correspond au nombre de chemin qui passent par \(k\) succès (ou échecs) dans un arbre à \(n\) niveaux
Exemples :
- \(\displaystyle {4 \choose 0}=1\)
- \(\displaystyle {8 \choose 7}=8\)
- \(\displaystyle {5 \choose 2}=10\)
Calculer des coefficients binomiaux à l’aide du triangle de Pascal
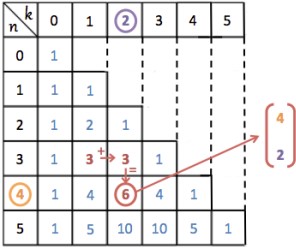
Calculer une probabilité dans le cas d’une loi binomiale
Lors de la répétition de n expériences suivant le schéma de Bernoulli (Succès \(s\) de probabilité \(p\) ou échec \(\overline{s}\) de probabilité \(1-p\) ), la probabilité d’obtenir \(k\) succès vaut
\(P(X=k) = \displaystyle {n \choose k} \times p^k \times p^{n-k}\)
où \(X\) est la v.a. qui compte le nombre de succès.