[vc_row][vc_column][vc_column_text el_id= »objectif-2″]

Fonctions – définition

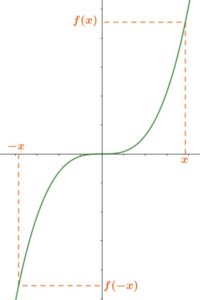
[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Une fonction $f$ associe à une valeur $x$ une autre valeur $y$.

On écrit $y=f(x)$

$y$ est l’image de $x$ par $f$

$x$ est l’antécédent de $y$ par $f$[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text]

Quizz :

On donne la fonction définie par $f(x)=x^2+3$.[/vc_column_text][vc_column_text]

[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

Quizz :

[/vc_column_text][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-3″]

Fonctions – graphique

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Dans un graphique, on note en ordonnée ($y$) les image des nombres de l’axe des abscisses ($x$), et on place tous les points de coordonnées $(x;f(x))$

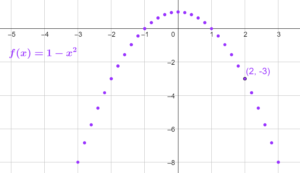
Par exemple, le point de coordonnées $(2;-3)$ est obtenu en calculant $f(2)=1-2^2=-3$[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

Quizz :

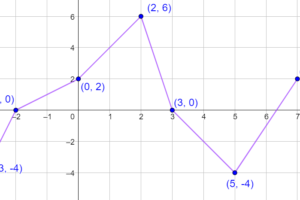
On donne la courbe suivante[/vc_column_text][vc_single_image image= »2627″ img_size= »300×200″ alignment= »center » style= »vc_box_rounded » onclick= »kalium_lightbox »][vc_column_text]Répondre aux 4 questions suivantes :[/vc_column_text][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-4″]

Fonctions – Équation $f(x)=k$

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Dans un graphique, on résout l’équation $f(x)=k$ en traçant une droite à la hauteur $k$ et en repérant les points d’intersection avec la courbe.

Les solutions se lisent sur l’axe des abscisses.

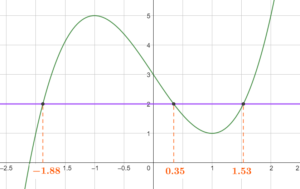
Par exemple, l’équation $f(x)=2$ admet 3 solutions. Valeurs approchées : -1,88 ; 0,35 ; 1,53[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text]

Quizz :

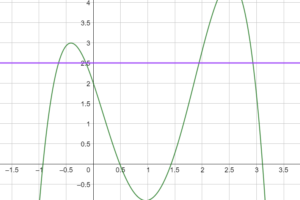
On donne la courbe suivante[/vc_column_text][vc_single_image image= »2645″ img_size= »300×200″ alignment= »center » style= »vc_box_rounded » onclick= »kalium_lightbox »][vc_column_text]Répondre aux 4 questions suivantes à l’aide du graphique :[/vc_column_text][vc_column_text]

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text el_id= »objectif-5″]

Fonctions paires et impaires

[/vc_column_text][/vc_column][/vc_row][vc_row content_placement= »middle »][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Une fonction paire vérifie pour tout $x$ : $f(-x)=f(x)$.

Sa courbe est symétrique par rapport à l’axe des ordonnées

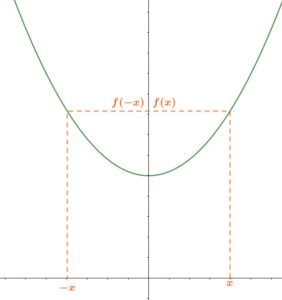
[/vc_column_text][/vc_column][vc_column width= »1/2″][vc_column_text el_class= »proprieteseconde propriete »]Une fonction impaire vérifie pour tout $x$ : $f(-x)=-f(x)$.

Sa courbe est symétrique par rapport à l’origine

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]

Plan de travail

[/vc_column_text][/vc_column][/vc_row][vc_row][vc_column][vc_single_image source= »external_link » onclick= »img_link_large » img_link_target= »_blank » custom_src= »https://docs.google.com/drawings/d/e/2PACX-1vT80q5efHgRaRQt8Ym4mgSVQAV_w_Z1e60qVSjZvQ2RGr5-dkI2Lx_BtNgPG43FPiqmH9MLhcuu_uef/pub?w=960&h=720″][/vc_column][/vc_row]